この章では、Pythonを使って実際に機械学習アルゴリズムを実装していきます。具体的には、線形回帰、ロジスティック回帰、k近傍法(KNN)、決定木とランダムフォレストについて解説します。それぞれのアルゴリズムには特徴があり、用途やデータの特性に応じて適切なものを選ぶことが重要です。
4.1 線形回帰
概要:
線形回帰は、最も基本的な回帰モデルであり、連続的なターゲット変数(例えば、家の価格や気温など)を予測するために使われます。このアルゴリズムは、与えられたデータの特徴(説明変数)とターゲット(目的変数)との間の関係を直線的なモデルで表現します。モデルは以下の形で表されます。
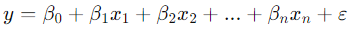
ここで、
- y はターゲット変数(予測される値)
- x1,x2,…xn は説明変数(予測に使われるデータの特徴)
- β0 は切片(モデルの初期値)
- β1,β2,…βnは各説明変数に対応する回帰係数
- εは誤差項です。
数学的背景:
線形回帰モデルは最小二乗法を用いて、与えられたデータに最も適合する直線を求めます。最小二乗法は、予測値と実際のターゲット値との誤差(二乗誤差)の合計を最小化する係数を見つける手法です。具体的には、次の目的関数を最小化します。
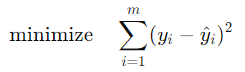
ここで、
- yiは実際の値
- y^i は予測された値です。
実装例(Pythonコード):
Pythonで線形回帰を実装するには、scikit-learnライブラリが便利です。以下のコード例では、sklearn.linear_modelのLinearRegressionクラスを使用して線形回帰モデルを構築し、予測を行います。
# ライブラリのインポート
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# データの準備(例としてランダムに生成されたデータを使用)
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# 訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# モデルの構築と訓練
model = LinearRegression()
model.fit(X_train, y_train)
# 予測
y_pred = model.predict(X_test)
# モデルの評価
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
print(f"予測精度(RMSE): {rmse}")
解説:
LinearRegressionクラスは、線形回帰モデルを提供するもので、fitメソッドでデータに適合させます。- データはランダムに生成したものを使用していますが、実際には家の価格予測などの現実的なデータを使用できます。
train_test_split関数でデータを訓練用とテスト用に分け、モデルが適合していないデータで予測性能を評価します。- 最終的に、モデルの性能を評価するためにRMSE(Root Mean Squared Error)を算出しています。RMSEは値が小さいほど予測精度が高いことを示します。
4.2 ロジスティック回帰
概要:
ロジスティック回帰は、分類問題に使用されるアルゴリズムで、ターゲット変数が2つ以上のカテゴリに分類される場合に適しています。特に、二項分類(バイナリ分類)問題でよく用いられ、例えば、あるメールがスパムかどうか、ある患者が病気かどうかなどの予測に使用されます。
ロジスティック回帰は名前に「回帰」と含まれますが、分類アルゴリズムです。ロジスティック関数(シグモイド関数)を使用して、出力が0から1の間の確率値として表されます。
ロジスティック関数は以下のように定義されます。
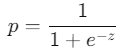
ここで、
- p は予測される確率
- z は説明変数とその係数の線形結合です。
数学的背景:
ロジスティック回帰は線形回帰と同様に、説明変数の線形結合を使ってターゲット変数を予測しますが、その結果をシグモイド関数に通すことで、出力が0から1の範囲に収まるようにします。この確率を基に、出力が0.5以上なら「1(肯定)」、それ未満なら「0(否定)」と分類します。
ロジスティック回帰の目的関数は対数尤度関数を最大化することです。
実装例(Pythonコード):
ロジスティック回帰の実装もscikit-learnライブラリを使って行います。以下の例では、sklearn.linear_modelのLogisticRegressionクラスを使ってバイナリ分類を実行します。
# ライブラリのインポート
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix
# データセットのロード(乳がんデータセットを使用)
data = load_breast_cancer()
X = data.data
y = data.target
# 訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# ロジスティック回帰モデルの構築と訓練
model = LogisticRegression(max_iter=10000)
model.fit(X_train, y_train)
# 予測
y_pred = model.predict(X_test)
# モデルの評価
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
print(f"分類精度: {accuracy}")
print("混同行列:")
print(conf_matrix)
解説:
- 乳がんデータセットを使い、良性か悪性かを分類します。このデータセットは
scikit-learnに組み込まれたものを使用しています。 LogisticRegressionクラスを使ってモデルを構築し、fitメソッドで訓練します。- 予測された結果と実際のターゲット値を比較して分類精度を測定します。また、混同行列を使って各クラスの正解率と誤分類を分析します。
4.3 k近傍法(KNN)
概要:
k近傍法(k-Nearest Neighbors, KNN)は、最もシンプルな分類アルゴリズムの一つで、非パラメトリックな手法です。訓練データのラベル付きデータポイントに基づいて、未知のデータポイントのカテゴリを予測します。k近傍法では、新しいデータポイントが既知のデータポイントにどれだけ近いか(距離に基づいて)を評価し、最も近いk個のデータポイントのラベルで新しいデータポイントを分類します。
数学的背景:
k近傍法では、ユークリッド距離やマンハッタン距離などを使ってデータポイント間の距離を計算します。次に、訓練データの中で最も近いk個のデータポイントのラベルを数え、多数派のクラスに新しいデータポイントを分類します。
ユークリッド距離は次の式で計算されます。
.png)
ここで、
- p と q は2つのデータポイント
- n は次元数です。
実装例(Pythonコード):
KNNの実装もscikit-learnを使います。次の例では、sklearn.neighborsのKNeighborsClassifierクラスを使ってKNNによる分類を行います。
# ライブラリのインポート
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy
# データセットのロード(アヤメデータセットを使用)
data = load_iris()
X = data.data
y = data.target
# 訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# k近傍法(k=3)のモデルの構築
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)
# 予測
y_pred = knn.predict(X_test)
# モデルの評価
accuracy = accuracy_score(y_test, y_pred)
print(f"分類精度: {accuracy}")
解説:
- アヤメデータセット(Iris dataset)を使用して、KNNによる分類を行います。このデータセットには3つのクラス(アヤメの品種)があり、4つの特徴(がく片と花弁の長さ・幅)が含まれています。
KNeighborsClassifierクラスを使って、k=3のモデルを構築します。これは、新しいデータポイントを3つの最も近いデータポイントのラベルに基づいて分類するという意味です。- モデルの性能は、分類精度で評価します。精度は、テストデータに対して正しく分類されたデータポイントの割合を示します。
k近傍法の特徴と使いどころ:
- シンプルで直感的: 訓練データをそのまま使用し、複雑なモデルの学習が不要です。非線形な分類問題にも対応できます。
- 訓練フェーズがない: 他のアルゴリズムとは異なり、KNNはモデルの訓練を必要とせず、新しいデータポイントが現れるたびにその都度計算を行います。そのため、訓練は高速ですが、予測が遅くなる場合があります。
- 計算量が多い: 大量のデータセットに対しては、予測フェーズで距離計算が多くなり、計算コストが高くなるため、大規模データには向きません。
- ノイズに敏感: kの値を適切に選ばないと、ノイズに影響されて誤分類が増える可能性があります。
4.4 決定木とランダムフォレスト
4.4.1 決定木
概要:
決定木(Decision Tree)は、回帰問題や分類問題の両方に使用できるアルゴリズムで、データを分割しながら予測を行います。木構造でデータを分類することで、各ノードでデータを2つのグループに分割し、最終的には葉ノードに達した時点でクラスを予測します。決定木は直感的で解釈が容易なモデルです。
数学的背景:
決定木の構築は、データセットを条件付きで分割していくプロセスです。分割の基準として、Gini不純度やエントロピー、または回帰問題の場合は分散の減少などを使用します。たとえば、Gini不純度は以下のように定義されます。
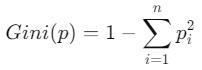
ここで、
- piは各クラスに属するデータの割合です。
Gini不純度が小さいほど、データの純度が高く、そのノードでのクラス分類が明確であることを意味します。
実装例(Pythonコード):
決定木はsklearn.treeモジュールのDecisionTreeClassifierを使って実装できます。
# ライブラリのインポート
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import classification_report
# 決定木モデルの構築
tree_model = DecisionTreeClassifier(random_state=42)
tree_model.fit(X_train, y_train)
# 予測
y_pred_tree = tree_model.predict(X_test)
# モデルの評価
print(f"分類精度: {accuracy_score(y_test, y_pred_tree)}")
print("詳細な評価:")
print(classification_report(y_test, y_pred_tree))
解説:
DecisionTreeClassifierクラスを使って決定木モデルを構築します。fitメソッドで訓練データに適合させ、predictメソッドでテストデータに対して予測を行います。- モデルの評価には分類精度とともに、詳細な分類結果を示す
classification_reportを使用し、クラスごとの精度、再現率、F1スコアを確認できます。
決定木の特徴と使いどころ:
- 解釈が容易: 決定木はグラフィカルに表現でき、どの条件でデータが分割されたかが明確に理解できます。
- 非線形な問題にも対応: 決定木は線形な決定境界に制約されないため、複雑な非線形問題に適しています。
- 過学習しやすい: 小さなデータセットや深い木構造を持つ場合、モデルが訓練データに過剰に適合し、汎化性能が低下することがあります。
4.4.2 ランダムフォレスト
概要:
ランダムフォレスト(Random Forest)は、複数の決定木を使ったアンサンブル学習手法です。複数の木から予測を行い、その結果を投票や平均化することで、単一の決定木よりも高い精度と汎化性能を実現します。
数学的背景:
ランダムフォレストは、決定木のブートストラップサンプル(訓練データからランダムに重複を許してサンプルを選ぶ方法)を使って個々の木を学習させます。各木は異なる特徴のサブセットを使って訓練され、最終的に多数決によって最も支持されたクラスを予測します。
ランダムフォレストでは、バギング(Bootstrap Aggregating)という手法を用いて予測のバラつきを減らし、より安定したモデルを作ります。
実装例(Pythonコード):
ランダムフォレストはsklearn.ensembleモジュールのRandomForestClassifierを使って実装できます。
# ライブラリのインポート
from sklearn.ensemble import RandomForestClassifier
# ランダムフォレストモデルの構築
forest_model = RandomForestClassifier(n_estimators=100, random_state=42)
forest_model.fit(X_train, y_train)
# 予測
y_pred_forest = forest_model.predict(X_test)
# モデルの評価
print(f"分類精度: {accuracy_score(y_test, y_pred_forest)}")
print("詳細な評価:")
print(classification_report(y_test, y_pred_forest))
解説:
RandomForestClassifierクラスを使って、ランダムフォレストモデルを構築します。n_estimators=100は、100本の決定木を作るという意味です。- モデルを訓練し、テストデータで予測を行います。
- 決定木と同様に、モデルの性能を分類精度と詳細なレポートで評価します。
ランダムフォレストの特徴と使いどころ:
- 高い精度: アンサンブル学習により、単一の決定木に比べて予測精度が向上します。
- 過学習に強い: 複数の木を使うことで、過学習を抑えつつ高い汎化性能を持つモデルを作ることができます。
- 並列処理が可能: 各決定木が独立して構築されるため、並列処理によって計算効率を向上させることができます。
まとめ
この章では、Pythonを使って線形回帰、ロジスティック回帰、k近傍法、決定木、ランダムフォレストの各機械学習アルゴリズムを実装しました。それぞれのアルゴリズムには異なる特性があり、適切な場面で使い分けることが重要です。
- 線形回帰は、連続値の予測に適しており、データが線形関係にある場合に有効です。
- ロジスティック回帰は、二項分類問題に適しており、確率的な分類を行います。
- k近傍法は、シンプルなアルゴリズムであり、距離に基づいた分類が得意です。
- 決定木は、解釈が容易で、非線形な問題に対応できますが、過学習に注意が必要です。
- ランダムフォレストは、アンサンブル学習によって安定した高精度のモデルを作ることができます。
これらのアルゴリズムを理解し、実際にPythonで試すことで、機械学習の基本的な実装スキルを身に着けることができます。